1. Bayes Theorem (Định lý Bayes)
\begin{aligned}
P(A\mid B) &= \frac{P(B\mid A)P(A)}{P(B)}
\end{aligned}
\\
\begin{align*}
\\
&P(A\mid B): \text{Xác suất xảy ra A biết B đã xảy ra rồi}\\
&P(B\mid A): \text{Xác suất xảy ra B biết A đã xảy ra rồi}\\
&P(A): \text{Xác suất xảy ra A}\\
&P(B): \text{Xác suất xảy ra B}\\
\end{align*}
Các biến thể của Naive Bayes:
- Multinomial Naive Bayes: Input đầu vào là các giá trị rời rạc bằng số lần các giá trị xuất hiện trong đoạn text.
- Bernoulli Naive Bayes: Các từ được xác định bằng việc chúng xuất hiện hay là không.
- Gaussian Naive Bayes: Input đầu vào là biến liên tục + giả thuyết phân phối chuẩn.
2. Decision Tree (Cây quyết định)
Thuật toán được hình thành từ các Decision Node và Leaf Node, và 1 node đặc biệt là Root Node.
Việc xây dựng thuật toán dựa vào nhiều yếu tố:
- Độ sâu của tree.
- Độ lệch của
Leaf Nodekhi đưa ra quyết định tối thiểu là bao nhiêu, độ lệch càng lớn càng tốt để chắc chắn về dự đoán. - Mỗi
Decision Nodenên chọn những feature nào để có thể đặt câu hỏi, phân nhánh dữ liệu. Nên chọn các feature sao cho phân tách dữ liệu càng lệch càng tốt. Cách phổ biến để lựa chọn feature là sử dụng Gini Impurity.
\begin{aligned}
\text{Gini Impurity}\\
\\
Gini = 1 - \sum_{i=1}^C(P_i)^2
\end{aligned}
\\
\begin{align*}
\\
&C: \text{Tổng số lượng class}\\
&P_i: \text{Xác suất 1 phần tử thuộc về class i}
\end{align*}
- Nếu 1 feature giúp phân chia node càng lệch thì Gini càng thấp và ngược lại. Gini thấp nhất là = 0, cao nhất là = 0.5, càng thấp càng tốt, càng cao càng tồi.
Ví dụ về việc áp dụng công thức, ta có 5 người chia làm 2 class có cho vay và không cho vay. Có 3 người là không cho vay và có 2 người là không cho vay. Xác suất cho vay là 40%, xác suất không cho vay là 60%. Áp dụng công thức ta có:
\begin{aligned}
&1- (0.4^2 + 0.6^2) = 0.48
\\
&\text{Đây là 1 giá trị khá tồi do nó gần 0.5 => phân chia đồng đều}
\end{aligned}Ngoài sử dụng Gini Impurity, ta còn có thể sử dụng Entropy để quyết định xem ở mỗi Decision Node, feature nào là tốt nhất:
\begin{aligned}
Entropy = \sum_{i=1}^C - P_i * \log_2(P_i)
\end{aligned}Ngoài ưu điểm dễ nhìn và trực quan, Decision Tree còn 1 số nhược điểm sau:
- Rất dễ bị overfitting khi cây quá sâu, quá nhiều level.
- Chỉ 1 thay đổi nhỏ của data cũng dẫn đến thay đổi cả cấu trúc tree.
- Ít được sử dụng trong bài toán Regression vì rất khó để tìm được điểm cân bằng giữa overfitting và underfitting (dữ liệu quá phức tạp còn mô hình quá đơn giản nên không đủ khả năng tổng quát hóa xu hướng dữ liệu).
Dùng trong bài toán nào thì Decision Tree dùng 1 mình sẽ có độ chính xác không cao, do đó sẽ kết hợp nhiều Decision Tree lại với nhau để tăng độ chính xác.
3. Random Forest (rừng ngẫu nhiên)
Random Forest sẽ tổng hợp các dự đoán của nhiều Decision Tree để đưa ra dự đoán cuối cùng.
- Với Classification sẽ dùng Majority Vote, nghĩa là class nào được đa số vote thì sẽ được chọn làm Final Prediction.
- Với Regression sẽ dùng Averaging, nghĩa là lấy giá trị trung bình của các dự đoán của Decision Tree để tìm Final Prediction.
Để việc kết hợp Decision Tree có ý nghĩa thì mỗi chúng phải được huấn luyện trên 1 bộ dữ liệu khác nhau để tránh việc tất cả học và đưa dự đoán giống hệt nhau. Để có nhiều bộ data khác nhau ta cần áp dụng Boostrapping để lấy mẫu có hoàn lại. Từ bộ data ban đầu, lấy mẫu có hoàn lại nhiều lần để tạo bộ dữ liệu con rồi đem đi huấn luyện nhiều Decision Tree.
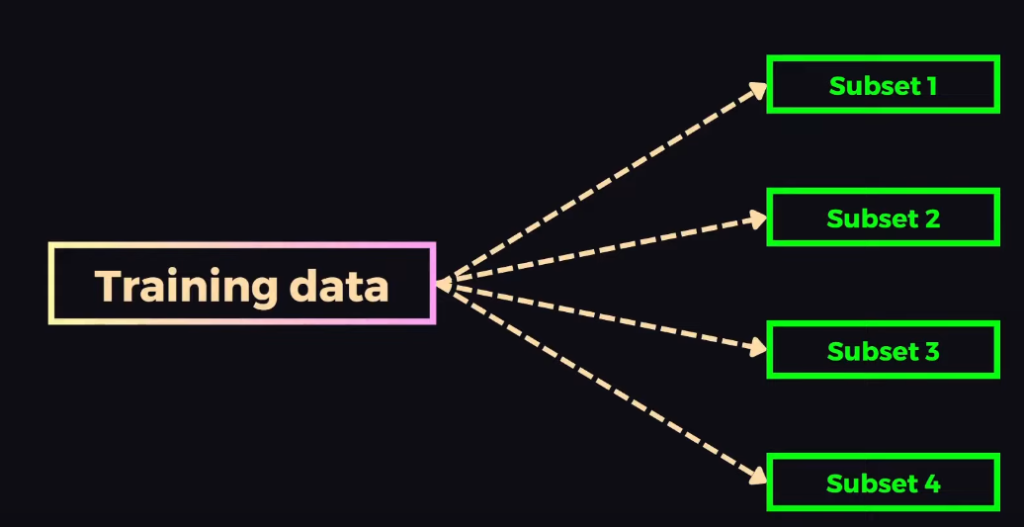
Một lưu ý là mỗi Decision Node chỉ được chọn feature tốt nhất trong 1 tập con của các feature để tăng độ đa dạng dự đoán.
Random Forest có tính giải thích thấp hơn. Tính giải thích là sau khi dự đoán cuối cùng có thể quay lại giải thích tại sao mô hình lại có dự đoán đó. Random Forest cũng tốn nhiều thời gian và tài nguyên hơn do ta phải huấn luyện nhiều Decision Tree cùng lúc.
4. Support Vector Machine
Mục tiêu của SVM trong bài toán classification là tìm ra 1 đường phân cách tốt nhất để phân chia các điểm dữ liệu của các class khác nhau trong không gian đa chiều.
Để là 1 đường phân cách tốt nhất thì cần thỏa mãn 2 điều kiện:
- Cách đều các điểm gần nhất của 2 class gọi là Margin.
- Margin được tạo ra là tối đa.
Các điểm dữ liệu gần đường phân cách tối ưu nhất của các class gọi là Support Vector vì nó sẽ quyết định công thức tính đường phân cách tối ưu. Các đường phân cách gọi là Hyperplane (siêu phẳng), đường phân cách tối ưu được gọi là Optimal Hyperplane (siêu phẳng tối ưu).
Trong các bộ dữ liệu thực tế sẽ có 2 cách thức mà SVM sẽ phải đối mặt:
- Không phải lúc nào cũng tìm được đường phân cách tối ưu để phân chia hoàn hảo các điểm dữ liệu mà không sai sót chút nào. Để khắc phục ta sẽ chọn 1 giá trị là Hyperparameter gọi là C. C là ngưỡng mà SVM sẽ chấp nhận là sẽ sai miễn là dưới C là được.
- Không phải lúc nào dữ liệu cũng được phân chia 1 cách tuyến tính. Nghĩa là trong 2D không phải lúc nào cũng kẻ được 1 đường thẳng để có thể phân chia dữ liệu về 2 phía của đường thẳng. Lúc này sẽ áp dụng kỹ thuật gọi là Kernel Trick để đưa từ 2D lên nhiều chiều hơn để dễ phân chia tuyến tính.
SVM có hiệu năng cao, làm việc tốt với data nhiều chiều. Nhưng nó sẽ chậm chạp khi áp dụng lên data có quá nhiều data point.